Partial Fractions Integral 1

One of my students one day asked me to come up with some practice problems for partial fractions integrals. Soon after that, while camping, I challenged myself to come up with a long-ish one with integer solutions for the unknown constants. I came up with this:

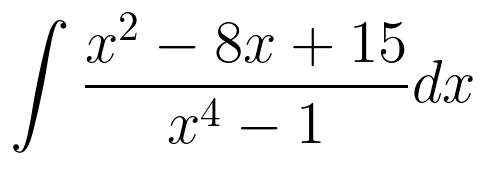
To solve this, the first thing we’d want to do is fully factor the denominator:

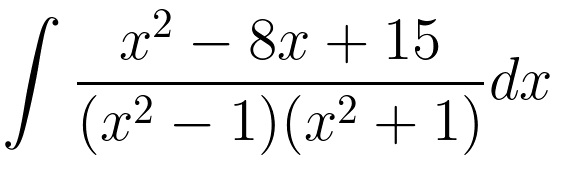
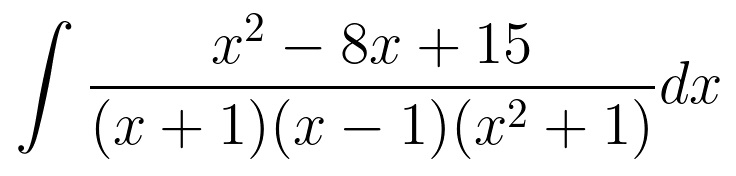
Two of our factors are linear, and one is quadratic. Reminder that these are treated differently in the partial fractions setup (the numerator isn’t always a constant–it’s a polynomial that has a power 1 less than the denominator).

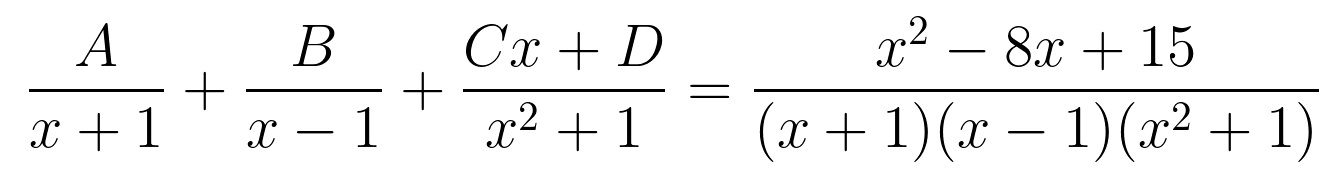
We want these fractions to have common denominators. I’ll sometimes describe this to my students as “multiply by what the fraction doesn’t have.”

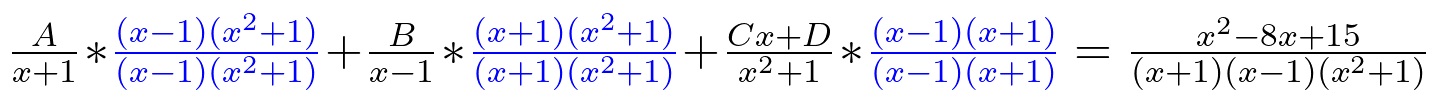
Now that everything has a common denominator, we can multiply both sides by said denominator to cancel them out. Then we can FOIL and expand what’s left:

It’s nice from here to organize the terms by their power of x, like this:

Here’s some color to emphasize why I like this:

For these two sides of the equation to be equal, they need to have the same number of x cubeds, x squareds, etc. The coefficients need to be equal. This leads to four equations that we can use to solve for the unknowns:

From here, it can be tricky to solve without some experience in matrix math or linear algebra (although there’s a fairly easy way to solve on a TI-84 that I may cover another time). The main goal is to add up the rows to cancel out variables. Luckily, in this case, we can add up all the rows to cancel out everything but B.

Plugging this answer into the first and third rows allows us to solve for A and C, and we can solve D from there:

Great :) now we can plug all 4 answers into the integral to get new integrals:

The first, second, and fourth of these integrals are fairly standard, and should probably be memorized in order to succeed in your calc 2 class. The third integral can be solved with a pretty quick u-substitution. The final result should be:

This is my second post here. For my first post, my work was shown through handwriting, but here, I tried out an equation editor. Feedback on which is preferred and how else I can improve these posts is always appreciated :)