Kite Area Optimization

Let’s say we have 4 metal rods, 2 of length a and 2 of length b. We want to arrange these metal rods into a kite. How long should the diagonals of the kite be to produce the largest possible area? What is that resulting area?

Fist, let’s draw the situation:

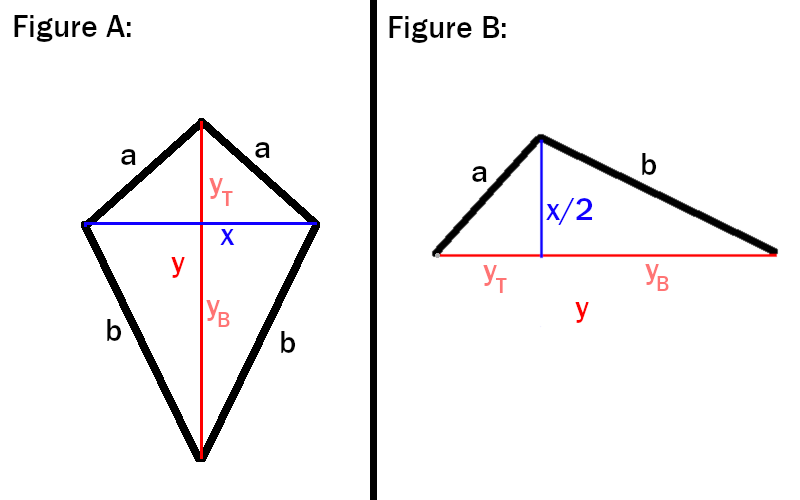
Figure A shows the entire kite, and figure B shows half of the kite, which, in my opinion, makes it easier to see how to find essential parts to this problem. Note that the longer diagonal, y is split up into two parts: y-top and y-bottom.

The area of a triangle is half the product of the base and height, so the area of the triangle in figure B is 1/2 · y · x/2. Since that triangle is half of the entire kite, multiplying this area by 2 gives us an equation for the area of the kite:

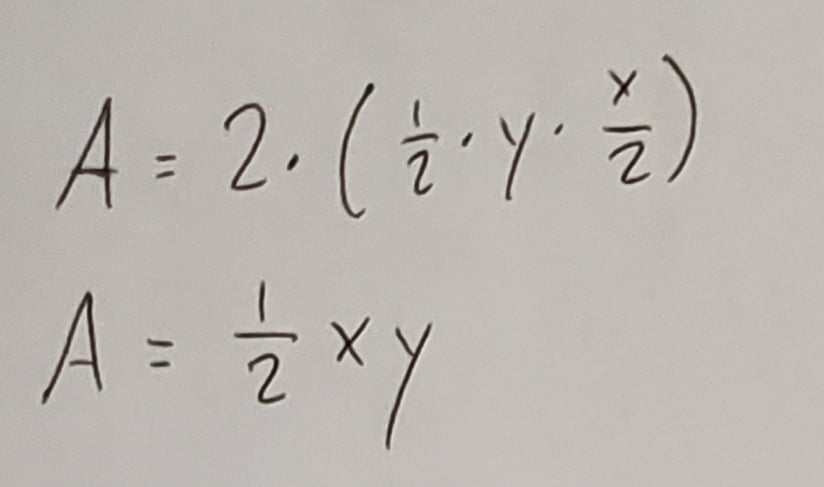
Using the Pythagorean theorem, we can find y-top and y-bottom in terms of x:

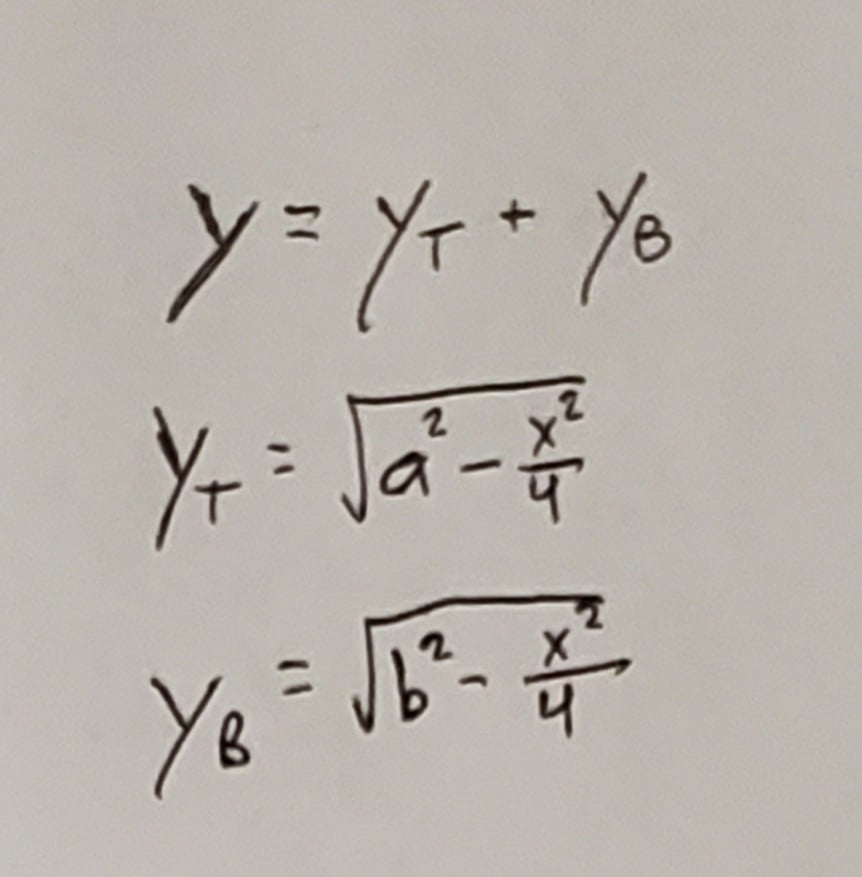
We can then plug these into our area equation from earlier:

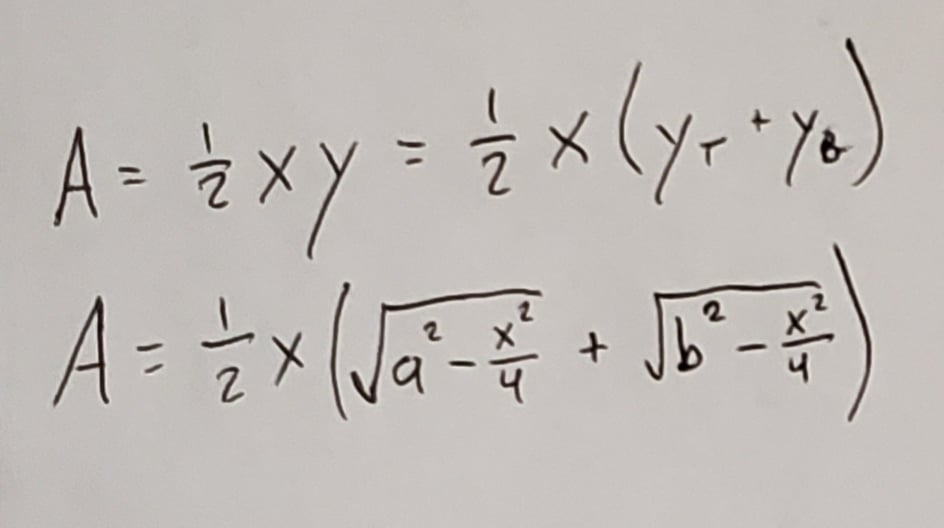
Now we have an equation to find the kite’s area only using x, which we can call A(x). To find the maximum value of A(x), we need to take the derivative, which in this case requires both the product and the chain rules:

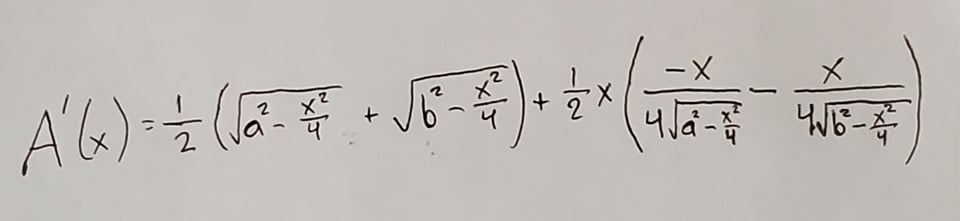
Our goal now is to set this new equation equal to 0 and then solve for x. The first thing I did was factor a -1 out of the second part of the equation, and I also noticed that you can multiply both sides of the equation by 2 to cancel out the halves:

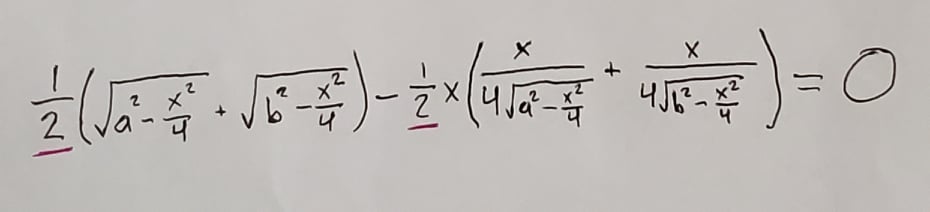
From there it takes a bit of adding, subtracting, multiplying, and dividing to solve, but at least a few things cancel out along the way:

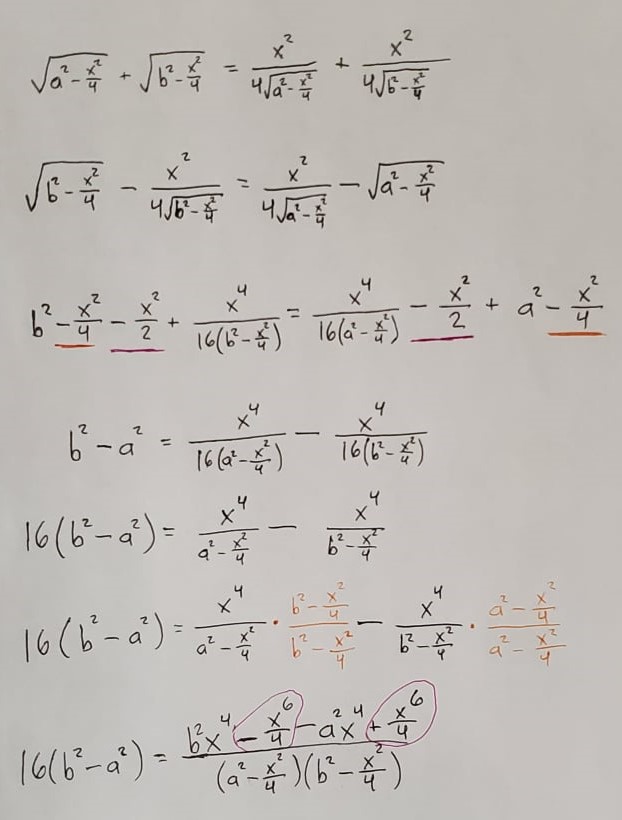
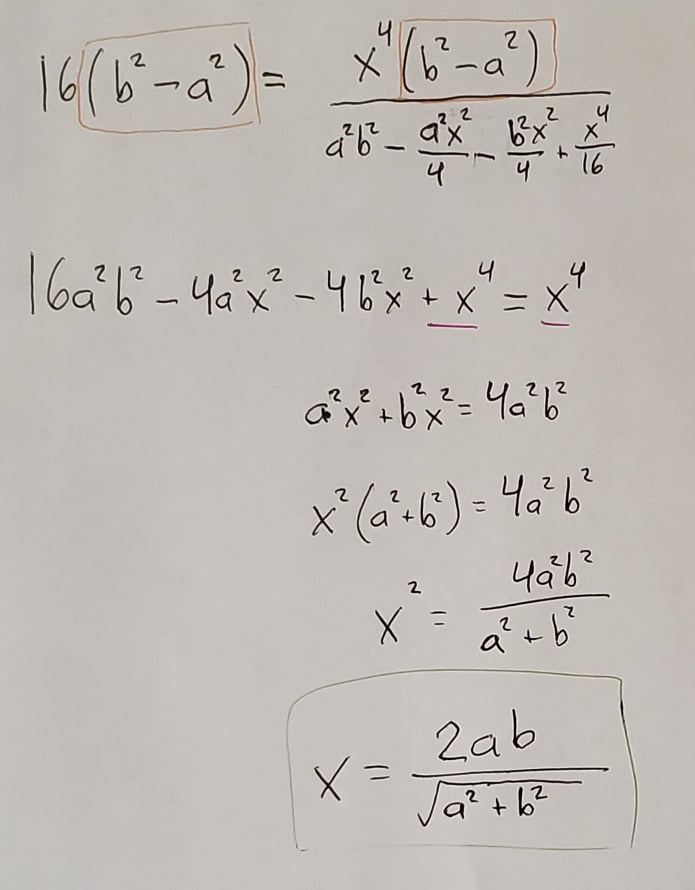
There we go! We solved for x. We can use this equation to also solve for y and the maximum possible area:

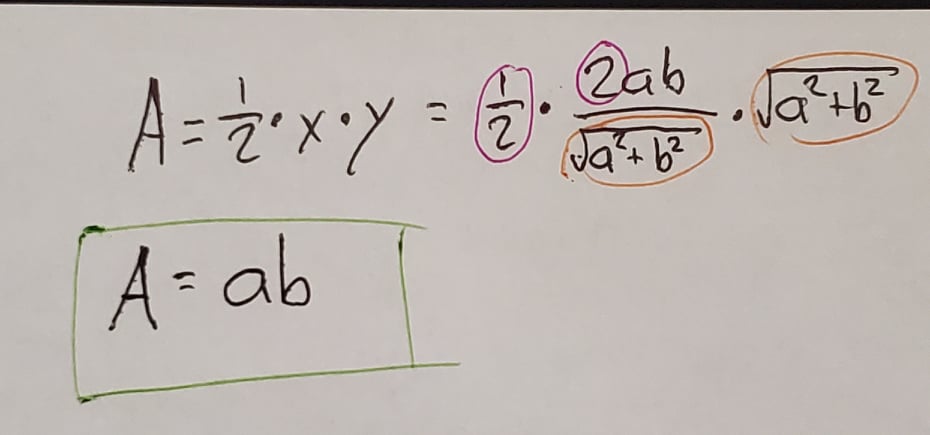
I also like to check my answers on Desmos, and these equations check out for multiple values of a and b:

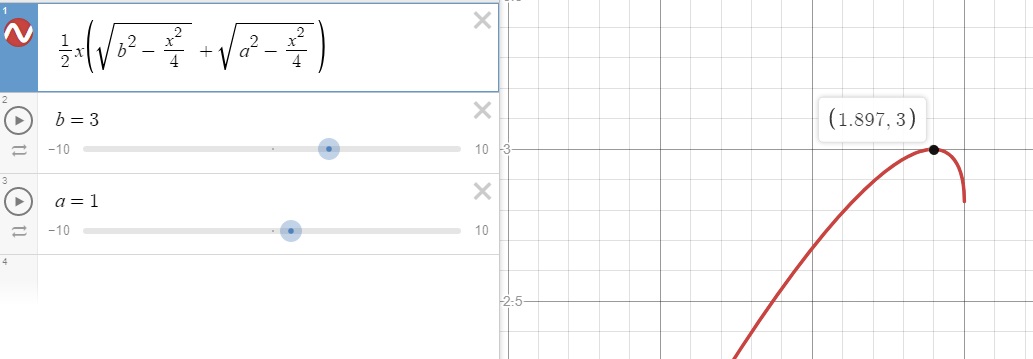
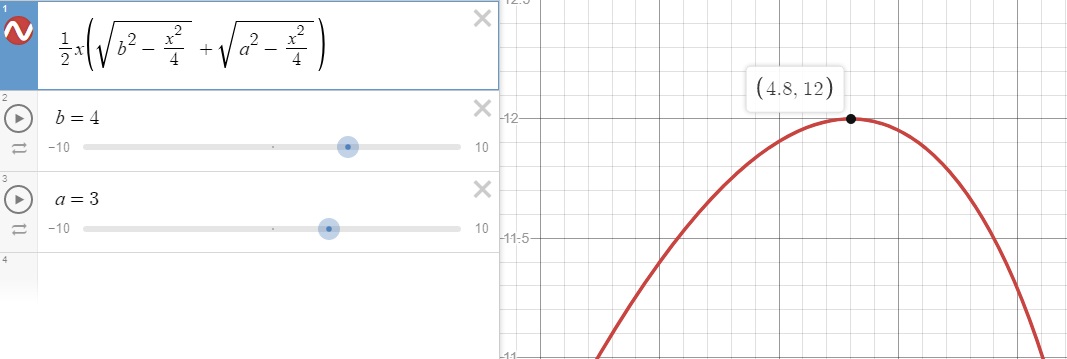
I hope this wasn’t too difficult to follow, this being my first post and all. This problem seemed like a good place to start since I had a hard time finding any other decent solutions online. I may revisit this post if I end up improving at this.