Inverse Tangent U-Sub

I see a lot of students struggling to see when an integral is related to inverse trig. Let’s take a look at the inverse tangent in this post. If an integral can be written like this: then that’s a good indication, but not a guarantee, that you should do a u-sub where u=f(x).

For example, this: can be rewritten as this:

So, like I said above, this is a good sign we should try doing a u-sub where u equals the thing that’s being squared.

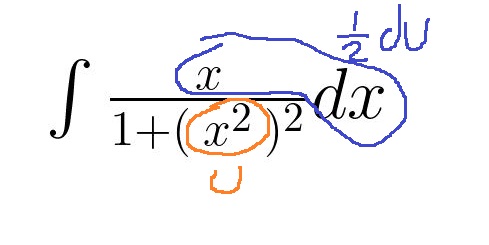
Now this is in the perfect form to take the integral and plug in the original value of u:

Keep in mind, though, that this isn’t always how to solve integrals that can be rewritten like shown above. Let’s take a look at a very similar integral:

We could rewrite the denominator the same way we could in the previous example, since it’s the exact same denominator and all. However, that isn’t the correct strategy to use here. If the numerator is a constant multiple of the derivative of the denominator, our u-sub should be setting u equal to the entire denominator:

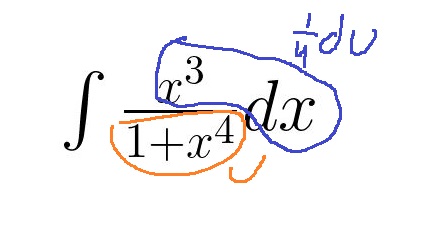
From here, we can take the integral and plug back in:

So, while you’re learning this, it’s more important to remember all the potential strategies than to pick the correct strategy on your first try. If you were to try the inverse tangent strategy on the second example here, it would not work, but it would only set you back like a minute or two as long as you try again with a different strategy. Integrals can be tricky, but that’s what I think makes them fun to solve :)